Probability is the study of chance. I would argue that for most people, probability and statistics are the most important subset of mathematics after algebra. I believe it’s a failure of the United States education system that high school students spend two years learning trigonometry and calculus, which will only be utilized by a select few students, but only touch on probability and statistics, which permeate almost every aspect of life in the modern world.
In the AV business, we are continually tasked with probabilistic and statistical tasks like deciding which projects to bid on, determining the probability of closing a deal, analyzing room data statistics, and searching for correlations.
But we don’t always apply the underlying mathematical methods of expected value, decision trees, confidence intervals, or scenario analysis to help us make optimal decisions.
There are 365 days in a year. There is a .27% chance that you share your birthday with any random individual. However, in a room of just 23 people, there is a 50/50 chance of two people sharing the same birthday.
In a room of 75, there is a 99.9% chance of at least two people matching.
A miracle is often defined as a one-in-a-million event. Let’s assume a human is alert for roughly eight hours per day and during this alert phase a human will see or hear one “event” per second, which may be either exceptional or unexceptional.
Under these assumptions, a human will experience a one-in-a-million event once every 35 days, on average.
So, the seemingly miraculous event is actually not uncommon at all once you have a large enough sample space. This phenomenon is known as Littlewood’s law.
Here’s another nonintuitive probability brain teaser referred to as the Monty Hall problem.
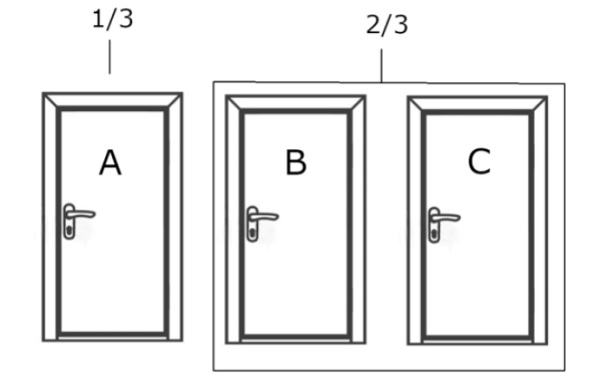
Suppose you’re on a game show and you’re given the choice of three doors. Behind one door is a car; behind the others, goats.
You pick a door, say door A, and the host, who knows what’s behind the doors, opens another door, say door C, behind which is a goat.
He then says to you, “Do you want to stay with your original choice, or would you like to select door B?”
Related: The AV MBA: What Great Thinkers Tell Us & How to Apply it to Your AV Business
Take a few seconds and think to yourself what your next move would be. Would you stay with your initial choice or switch to Door B?
In the Monty Hall problem, most people decide to stay with their initial choice.
When we were in middle school, many of us were told, “trust your gut” during tests. Andrew Campbell and Jo Whitehead from McKinsey Quarterly explain that “Our gut intuition accesses our accumulated experiences in a synthesized way, so that we can form judgments and take action without any logical conscious consideration.”
And this gut-trusting advice is often successful when you have familiarity with the problem or feedback from similar events.
But in the Monty Hall problem, I think our unfamiliarity with probability and our ingrained reliance on gut instincts sway contestants to stay with their initial choice. However, an understanding of probability suggests otherwise.
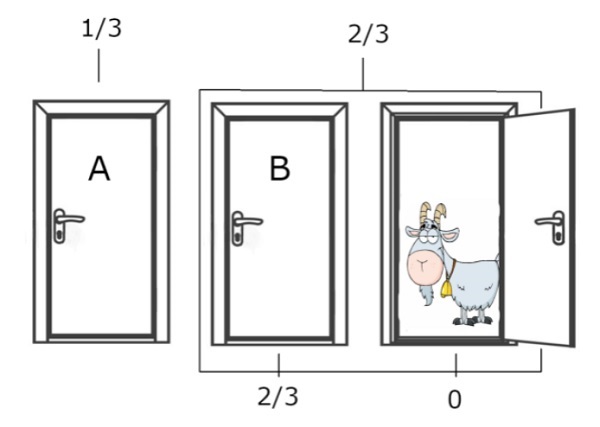
At the beginning of the game when all the doors were closed, you had a 1/3 chance of selecting the correct door and a ⅔ chance of being wrong.
Once the host opens one of the other doors to reveal a goat, the odds of your initial choice being correct remains at ⅓, but if you switch your odds of winning the car has increased to 2/3.
This solution is so counterintuitive that when the problem was published, nearly 1,000 PhDs wrote the author stating that he was incorrect. But it’s demonstrably true. You can play this game at home with a friend.
Grab three opaque cups, one coin, and a notepad. One person is the host, the other the contestant. As the host, have the contestant close their eyes, and place the coin under one cup.
“When a coincidence seems amazing, that’s because the human mind isn’t wired to naturally comprehend probability and statistics.” — Neil deGrasse Tyson
Have them select a cup at random, show them one of the non-selected cups that does not have the coin, and then force them to STAY with their initial bet.
After 30 trials, you will see that they selected the correct cup 1/3 of the time.
Repeat the experiment 30 more times, but instead of having them stay with their initial guess, force them to SWITCH.
You will see that by switching, they will have selected the coin 2/3 of the time.
As an industry, we need to not only understand probability, but implement them into our activities — for sales funnels, for scheduling logistics, for identifying a go/no-go.
In next month’s article we’ll dive a little deeper into how we can use probability tree analysis for optimal decision making in the audiovisual world.
But for now, know this: probability is incredibly relevant to the work we do, and even a beginner’s understanding of how to apply it in our industry can have incredibly useful applications for designing making in AV. Stay tuned!